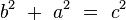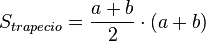Luisa Cáceres de Arismendi
| Luisa Cáceres de Arismendi | |
|---|---|
 | |
Datos personales | |
| Nacimiento | 25 de septiembre de 1799 |
| Fallecimiento | 28 de junio de 1866 (66 años) |
Luisa Cáceres de Arismendi (Caracas, 25 de septiembre de 1799 - Caracas, 28 de junio de 1866). María Luisa Cáceres Díaz (conocida por la historia como Luisa Cáceres de Arismendi) es uno de los personajes femeninos más insignes y heroína de la gesta de independencia de Venezuela. Esposa del General Juan Bautista Arismendi.
Luisa Cáceres De Arismendi nace en Caracas – Venezuela el día 25 de septiembre de1799, hija primogénita del matrimonio formado por el distinguido pedagogo José Domingo Cáceres y su esposa Doña Carmen Díaz fue bautizada en la Iglesia Santa Rosalía. Su padre, profesor de latín, se ocupó de enseñarle a leer y escribir, así como los principios y normas morales puestos a prueba durante los años de cautiverio y destierro de la joven patriota. Tuvo dos hermanos que la seguían se llamaban Félix y Manuel Cáceres.Biografía
Es educada para ejercer el sagrado ministerio de esposa y de madre. Por el atraso en que se encontraba la instrucción pública Colombiana de 1813 en esa época, su espíritu no fue cultivado, aprendiendo solamente a leer y a escribir y todas aquellas normas de sociabilidad que trasmitían los padres a los hijos desde lejanos tiempos. Pero a pesar de su escasa instrucción Luisa pudo elevarse a su destino y perfeccionarse moralmente durante su infancia.
Desde muy temprana edad Luisa Cáceres se distinguía por su hermosura. De estatura mediana y bellas facciones, llamaba la atención por su porte y gentileza. En el año de 1814, antes de cumplir los quince años de edad fue solicitada en matrimonio ante sus padres por un joven patriota, el entonces Coronel Juan Bautista Arismendi, viudo hacía pocos años de Doña María del Rosario Iralda.
Tragedia familiar
El año de 1814 fue un año adverso para la naciente República y también para la familia Cáceres; el 6 de marzo las tropas del realista Francisco Rosete asaltaron la guarnición de Ocumare y matan al padre de Luisa quien se encontraba allí por invitación de su amigo el comandante Juan José Toro. La Comandancia Militar, en Caracas, a cuyo frente se encontraba el coronel Juan Bautista Arismendi, organiza una expedición de jóvenes estudiantes y acude el día 14 en auxilio de los patriotas sitiados en Ocumare; entre los soldados de la expedición estaba Félix Cáceres, hermano de Luisa. Las tropas de Arismendi son derrotadas y Félix es hecho prisionero y ejecutado el 16 de marzo.
Por otra parte las sucesivas derrotas y la ofensiva de José Tomás Boves y de su “Legión infernal” obligan a las fuerzas patriotas a abandonar la plaza de Caracas; el 7 de julio de 1814 se emprende la retirada a oriente comandada por Simón Bolívar y José Félix Ribas (hecho conocido en la historia venezolana como Emigración a Oriente); entre los emigrados marcha la familia Cáceres, durante la travesía mueren 4 tías de Luisa y sólo quedan ella, su madre y un hermano menor. Los emigrados pasan por Barcelona y se dirigen a Cumaná a donde llegan a fines de agosto, pero la calma será por poco tiempo ya que Boves toma la ciudad.
Muchos de ellos consiguen pasar a Margarita donde Arismendi puede ofrecerles alguna seguridad. El coronel Arismendi busca a la familia Cáceres, a quienes había conocido y frecuentado por algún tiempo en Caracas en la Navidad de 1813, les proporciona vestido, alojamiento y demás recursos necesarios. El día 4 de diciembre de 1814 Luisa Cáceres contrae matrimonio con el coronel Juan Bautista Arismendi.
r]Presidio en La Isla de Margarita
Para el año de 1815 Arismendi es Gobernador provisional, momento en que a la isla de Margarita arribó El General Realista Pablo Morillo al frente de una escuadra como jamás nunca se había visto en las costas de Venezuela. El acoso español se inició por todo el territorio de la república, durante algunos meses viven en las afueras de La Asunción bajo el espionaje y la presión que las autoridades españolas mantienen sobre los simpatizantes de la causa patriota en la isla. En septiembre de 1815 se ordena apresar a Arismendi, éste escapa y se oculta con uno de sus hijos en las montañas de Copey; el día 24 de septiembre Luisa, quien se encontraba embarazada, es tomada como rehén para doblegar a su esposo y encerrada bajo la vigilancia en la casa de la familia Amnés, días después es trasladada a un calabozo del Castillo Santa Rosa en la Asunción. Es en ese calabozo oscuro y sin luz de la fortaleza que comienza el suplicio de Luisa por el maltrato y vejámenes cometidos por las tropas españolas ante los cuales nuestra heroína nunca cederá. Un centinela vigila hasta sus menores movimientos, y es obligada a comer el rancho que le dan como único alimento. Luisa permanece sentada noche y día sin moverse para no llamar la atención del celador. Un día el capellán de la fortaleza de regreso de sus oficios pasa por su puerta y se queda contemplando aquella mujer en actitud de vencida, de humillada. Movido a compasión por su estado logra que le lleven comida de su propia casa, que le supriman el centinela y que le coloquen una luz que ilumine el calabozo durante la noche.
Las acciones militares de Arismendi le permiten hacer prisioneros a varios jefes españoles entre ellos al comandante Cobián, de la fortaleza de Santa Rosa por lo cual el jefe realista Joaquín Urreiztieta propone a Arismendi canjear esos prisioneros por su esposa, tal ofrecimiento no es aceptado y el emisario recibe por respuesta: «Diga al jefe español que sin patria no quiero esposa». A partir de aquel momento empeoran las condiciones del cautiverio y se desvanece la posibilidad de libertad al fracasar los patriotas en un intento de asalto de la fortaleza. Habiendo trascurrido un mes desde su prisión oye una noche una gran alarma y se da cuenta de que se prepara un asalto al cuartel. La lisonjea la esperanza de un triunfo de los suyos pero al amanecer, cuando todo está en calma, sólo oye los lamentos de los moribundos y de los heridos de la refriega. Horas más tarde los soldados la sacan de su prisión para pasearla sobre la explanada del cuartel, donde han sido fusilados los infelices prisioneros. Luisa tiembla ante la idea de que ella también va a ser sacrificada, pero estaba equivocada: el objeto de sus verdugos era que se paseara por sobre los cadáveres de los patriotas fusilados, que caminara por sobre aquellos cuerpos sin vida que habían tenido la osadía de querer libertarla. La sangre derramada va a desembocar en el aljibe de la prisión y a Luisa la obligan a calmar su sed con aquella agua putrefacta y pestilente mezclada con la sangre de los suyos. El 26 de enero de 1816, Luisa da a luz una niña que muere al nacer dadas las condiciones del parto y del calabozo en el cual se encontraba prisionera.
Traslado a la prisión de la Guaira
Los brigadieres Juan Bautista Pardo y Salvador Moxó ordenan que se traslade a la detenida al fortín de Pampatar donde permanece algunos días, luego es trasladada a la prisión de La Guaíra y posteriormente al convento de la Inmaculada Concepción en Caracas, donde ingresa como prisionera el 22 de marzo de 1816. Durante todo este tiempo se le mantiene incomunicada y sin noticias de sus familiares. Los triunfos de las fuerzas republicanas comandadas por Arismendi en Margarita y por el general José Antonio Páez en Apure determinaron que el brigadier Moxó ordenara el traslado de Luisa a Cádiz, por tal razón es llevada de nuevo a la prisión de La Guaira el 24 de noviembre de 1816 y embarcada el 3 de diciembre. En alta mar son atacados por un buque corsario que se apodera de todo el cargamento y los pasajeros son abandonados en la isla de Santa María en las Azores.
Estadía en Cádiz
Imposibilitada de regresar a Venezuela, Luisa llega a Cádiz el 17 de enero de 1817. Es presentada ante el capitán general de Andalucía, quien protesta por la arbitraria decisión de las autoridades españolas en América y le da la categoría de confinada, le asigna una pensión de 10 reales en vellón diarios y confía su protección al médico José María Morón y su esposa Concepción Pepet, luego que pagan una fianza y se comprometen a presentarla mensualmente ante el juez de alzada. Durante su permanencia en Cádiz, se negó a firmar un documento donde manifestaba su lealtad al Rey de España y renegaba de la filiación patriota de su marido a lo cual respondió que el deber de su esposo era servir a la patria y luchar por libertarla. El destierro transcurre sin noticias de su madre y su esposo. En marzo de 1818 el teniente Francisco Carabaño y el inglés Mr. Tottem se ofrecen para ayudarla a trasladarse a América; se hacen todos los preparativos pertinentes para la fuga y la joven promete que su esposo pagará todos los gastos al arribar a tierra margariteña. Se despide de la familia Morón y emprende viaje a bordo de una fragata de bandera norteamericana.
Llegada a Filadelfia
El 3 de mayo de 1818 llega a Filadelfia donde conoce a la familia del general patriota Lino Clemente, emigrados a Estados Unidos, quienes le brindan amistad y apoyo. El coronel Luis Rieux, comisionado por Arismendi, visita a Luisa y se encarga de su traslado a Margarita a donde llega el 26 de julio de 1818. Posteriormente, el 19 de septiembre de 1819, el Consejo de Indias dicta una resolución mediante la cual se le concedía absoluta libertad y facultad de fijar su residencia donde quisiera. Residió en Caracas hasta el día de su muerte el 2 de junio de 1866, después de haber visto a su patria libre y la bandera de la libertad ondeando en la América antesespañola.
Honores
Sus restos fueron trasladados al Panteón Nacionalel 24 de agosto de 1876 convirtiéndose en ser la primera mujer cuyos restos reposan en el más alto altar de la Patria.
En la actualidad en la ciudad de Caracas un instituto técnico tiene su nombre "Instituto Técnico Luisa Cáceres de Arismendi".
En la ciudad de la Asunción capital del Estado Nueva Esparta existe la plaza Luisa Cáceres de Arismendi.
Su busto es la imagen del billete de 20 bolívares fuertes (BsF. 20) en el sistema monetario actual de Venezuela.
Existe el Hospital Pediatrico Luisa Cáceres de Arismendi, en el Complejo Hospitalario José Ignacio Baldo en Caracas.






 y
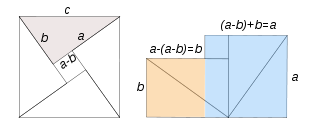
y  , y la medida de la hipotenusa es
, y la medida de la hipotenusa es  , se establece que:
, se establece que: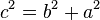









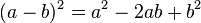
 .
.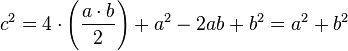

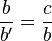


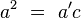
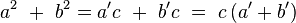
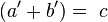 , por lo que finalmente resulta:
, por lo que finalmente resulta:


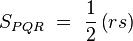
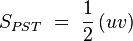
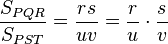
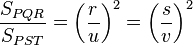
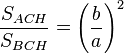
 (I)
(I)
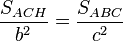
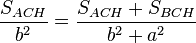 , así que:
, así que: